RNN 모델은 자연어처리의 연구과 함께 대두되었던 딥러닝 모델로 Sequence data를 처리하여 특정 Sequence data로 출력으로 변환하도록 훈련된 모델이다. Recurrent 방식은 입력값을 보존하여 기억할 수 있도록 하기에 문장 형식의 데이터나 시계열 데이터, 소리 데이터 등에 적절하게 이용되곤 했다. 하지만 몇가지의 치명적인 단점이 있으며 Transformer 기반의 모델이 등장하고 나서는 자연어 처리 분야에서 많이 사용되지 않고 있다. 그럼에도 불구하고 해당 방식을 Computer Vision이나 여러 알고리즘에서 사용하기에 충분히 집고 넘어가 볼 필요성이 있다.
우선 가장 심플한 버전인 Vanila RNN을 확인해자.

아마 공부를 했던 사람들에게는 아주 익숙한 장면일 것 같은데, 여기에서 g(x)는 Activation function으로 sigmoid보다 미분값의 최대가 더 큰 tanh일 때를 고려해보았고, f()는 현재 시점의 정보와 이전에 학습된 정보를 선형 결합하여 낸 결과이다. f를 통해 이전의 값을 고려하려는 시도를 볼 수 있고 다음 tanh를 통해여 얻은 결과는 미래 정보에 추가적인 정보로 들어가게 된다. 이때 확인되는 3가지의 Weight 값\( W_{th}, W_{hh}, W_{hy} \)들은 각각 동일한 값으로 존재하며, 만일 \( W_{xh} \) 중 하나의 값이 변경된다고 하면 모든 \( W_{xh} \)값이 동시에 동일하게 업데이트된다. (이러한 조건을 인지하고 다음 내용을 받아드려보자.)
그렇다면 현재(t)를 기준으로 과거의 값(1,2,...t-1)들이 현재의 결과에 미치는 정도는 얼마나 될까? 이를 확인하고 최적의 결과를 내기위해 모델은 Back Propagation을 수행하게 된다. Back Propagation이란 '오차 역전파'라고도 하며 동일 입력층에 대해 원하는 값이 출력되도록 개개의 가중치를 조절하는 방법으로 사용된다. 쉽게 말해서 각각의 입력값(\( x_1, x_2,...,x_t \))이 출력값(\( y_t \))에 알맞는, 원하는 영향을 주기위해 어떤 가중치(여기서 초점을 맞추려는 가중치는 \(W_{xh}\).)가 적당한지 확인하는 것이다. 하지만 Vanila RNN의 단점은 여기서 발견할 수 있다.
Back propagaion을 통해 가중치 값을 얻기 위해서는 편미분을 사용하는데 이는 아래와 같이 간단하게 표현해 볼 수 있다.

hidden cell을 2개만 고려한 아주 간단한 형태로 편미분으로 가중치를 확인하는 방법을 확인해보면 생각보다는 간단하다. \( W_{xh} \)는 동일한 값을 가지고 있지만 모든 입력값에 대해 존재하기에 입력값이 n개가 있으면 구해야 할 \( W_{xh} \)의 개수 또한 n개가 된다.
즉 입력값이 많아질수록 \( \dfrac{\partial y_t}{\partial W_{xh} \)의 식은 복잡해지는 것이다. 여기서 문제가 생긴다. 아래의 그림은 각 항에 대한 일반식과 Tanh 함수의 형태이다.
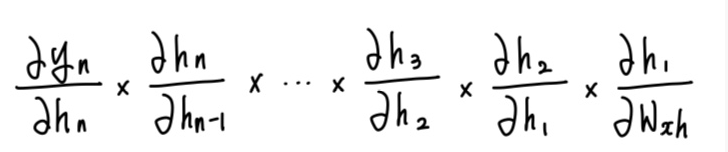

위에서 Activation function을 tanh로 설정하였다. 따라서 tanh의 미분값의 범위를 확인해보면 (0, 1]인 것을 계산을 통해 쉽게 알수 있다(맨 아래에 풀이있음). 그렇다면 임의의 t에 대하여 \( \dfrac{\partial y_t}{\partial W_{xh}} \)는 1 또는 (0,1)이며 (0,1)인 값이 n번 곱해진다면 결과값은 0으로 수렴하기에 Gradient Vanishing이 생긴다.(다른 활성화 함수를 사용했을 때 Exploding Gradient문제가 발생하기도 한다) 간단히 이야기를 하자면 유의미하던 안하던 입력값에 대한 가중치가 0으로(혹은 무한대로) 수렴(발산)하기에 학습이 잘 진행되지 않는다는 것이다. 이는 대량의 데이터로 학습할 시에 큰 악영향으로 다가오기에 자연어 처리 분야에서 잘 사용하지 않게 되었다.
이를 해결하기 위해 LSTM, GRU 등 많이 방식이 연구되었으며 이는 추후에 다뤄보고자 한다.
[ tanh 미분 풀이 및 시각화 ]
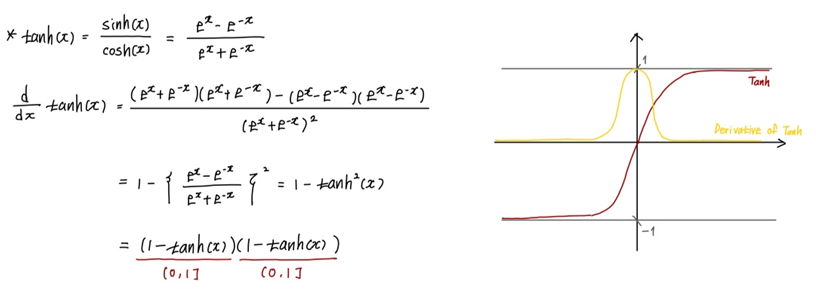
참고 사이트 :
1. Amazon Web Service - 순환 신경망(RNN)이란 무엇인가요?



